Massenstrom
Für den Ausdruck
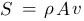 gilt
gilt
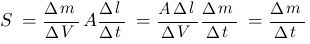
Es handelt sich also tatsächlich um eine Massenstromdichte. Weil
sie von den drei Größen (die oben multipliziert werden) abhängt, handelt es
sich aber auch um eine Funktion von drei Variablen. Die gesamte Massenstromdichte ist
konstant (d.h. 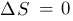 ), daher bedingt
eine Änderung einer der Variablen immer eine Änderung einer oder
beider weiterer Variablen (in der Summe bleibt die Fkt. konstant, die einzelnen
Beiträge heben sich gewissermaßen auf).
), daher bedingt
eine Änderung einer der Variablen immer eine Änderung einer oder
beider weiterer Variablen (in der Summe bleibt die Fkt. konstant, die einzelnen
Beiträge heben sich gewissermaßen auf).
Die Frage ist jetzt, wie sich die einzelnen Beiträge der Funktion
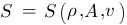 verändern, wenn sich eine der Variablen
verändert. Die Entwicklung einer Funktion mehrerer Variabler beschreibt
das totale Differential einer Funktion (mein Skript Mathe 2, ziemlich weit hinten).
In zwei Dimensionen sieht das so aus:
verändern, wenn sich eine der Variablen
verändert. Die Entwicklung einer Funktion mehrerer Variabler beschreibt
das totale Differential einer Funktion (mein Skript Mathe 2, ziemlich weit hinten).
In zwei Dimensionen sieht das so aus:
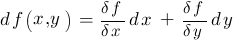
Benötigt werden die Ableitungen der Funktion nach jeweils einer der Variablen - die sind hier unhandlich. Das Logarithmieren ist ein einfacher Trick (Rechentechnik), um diese Ableitungen möglichst einfach durchführen zu können. Weil
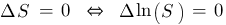
und
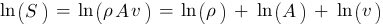
gilt für den speziellen Fall der konstanten Funktion
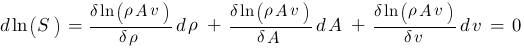
mit den Ableitungen
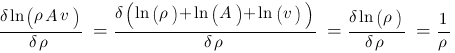
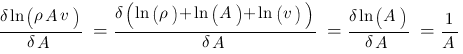
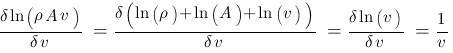
Die Ableitungen müssen jetzt nur noch in die Gleichung eingesetzt werden:
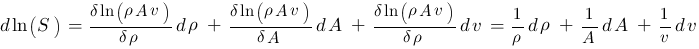
oder für makroskopische Änderungen
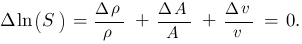
Genau da wollten wir hin, richtig?