Für ganze Zahlen
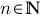 ist die Fakultät
ist die Fakultät
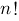 das Produkt aller positiven und ganzen
Zahlen von 1 bis
das Produkt aller positiven und ganzen
Zahlen von 1 bis 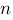 :
:
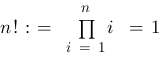 ·
·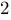 ·
·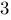 ·
·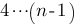 ·
·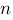
Beispiel zur Fakultät:
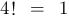 ·
·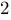 ·
·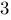 ·
·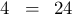
Als besondere Definition setzt man dabei (
warum denn?):
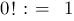
Unter einem Monom versteht man einen Ausdruck der Form
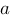 ·
·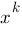 mit
mit 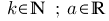 .
.
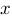 ist die Variable (sie muss nicht reell sein!)
ist die Variable (sie muss nicht reell sein!)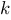 ist der ganzzahlige Exponent
ist der ganzzahlige Exponent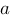 wird als Koeffizient bezeichnet
wird als Koeffizient bezeichnet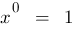 für alle
für alle
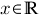
Ein Polynom ist eine (endliche) Summe von Vielfachen von Potenzen einer Variablen mit
natürlichzahligen Exponenten (üblicherweise mit
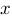 bezeichnet):
bezeichnet):
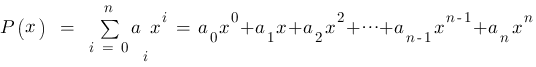
Als Grad des Polynoms wird der höchste Exponent 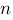 bezeichnet, für den der Koeffizient
bezeichnet, für den der Koeffizient 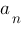 des Monoms
nicht null ist.
des Monoms
nicht null ist.
Beispielsweise ist 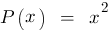 ein Polynom vom
Grad 2
ein Polynom vom
Grad 2
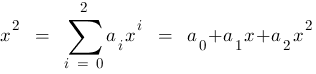
mit den Koeffizienten 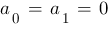 und
und 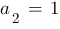
Der Fundamentalsatz der Algebra
besagt, dass ein komplexes Polynom vom Grad 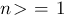 mindestens eine komplexe Nullstelle hat. Dann hat es genau
mindestens eine komplexe Nullstelle hat. Dann hat es genau
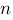 Nullstellen, wenn sie entsprechend
ihrer Vielfachheit gezählt werden. Jedes Polynom positiven Grades kann also
in ein Produkt von Linearfaktoren zerlegt werden.
Nullstellen, wenn sie entsprechend
ihrer Vielfachheit gezählt werden. Jedes Polynom positiven Grades kann also
in ein Produkt von Linearfaktoren zerlegt werden.
Rationale Zahlen sind reelle Zahlen, die sich als Verhältnis (lateinisch ratio) zweier
ganzer Zahlen darstellen lassen. Eine rationale Zahl kann also dargestellt werden als
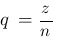 mit
mit 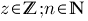 .
.
Der wichtigste Grund ist wohl, dass man beim Umgang mit Fakultäten Terme erhält, in denen durch 0! geteilt wird, die aber nicht divergieren dürfen.
Eine logische Begründung liefert das leere Produkt: es gibt genau eine Möglichkeit, nichts zu multiplizieren.